 |
 Dream Drive
-> Robot
Dream Drive
-> Robot
 |
|
|
二足歩行ロボットのモーション制御としてポーズとポーズの間を分割してつなぐといった方法がありますが、この分割された中間のポーズがやっかいなヤツで、実は思ったとおりの動きをしていません。
これはロボットのサーボが角速度で制御されているからです。 これを可能にするのが逆運動学です。 実は小型二足歩行ロボット程度の足の制御は高校数学+α(逆三角関数の基礎)で説明が出来ます。 これは、僕が解いてみた二足歩行ロボットにおける逆運動学の幾何学的解法です。
|
|
■ MENU ■
公開 2006.12.20 |
原点を腰に取り下方向をZ方向、前方をX方向に取るようなXYZ座標系で話を進めます。
精度に関しては足の長さの定数をmmでとって、倍精度で計算すれば、だいたいmm単位の制御は出来ます。 |
|
|
軸と角度の定義 各角度を定義する。 また足の長さを2aとし、腰から膝、膝から足の長さをそれぞれaとする。 ちなみにaは定数である。 |
|
|
|
||
|
|
膝の計算 腰から足までの直線距離を変数 l とおく。
x,y,zは目標値。 |
|
|
|
||
|
|
ピッチ軸の変位 体に対して、足裏が常に地面に平行であるためδ を計算する必要がある
xは与えられたx座標の変位である。 |
|
|
|
||
|
|
ピッチ軸の角度の決定 ここでピッチ角が決定する。
|
|
|
|
||
|
|
ロール軸の角度の決定 また、足裏が地面に平行であるには、ロール方向も同様に ε を計算することが必要
y,zは目標値である。 |
|
|
|
||
|
プログラムへの実装 いざ、プログラムに実装するわけですが、その計算はといえば引数をxyzと考えた場合、プログラム的な順番では下記の計算を毎ループ両足分計算することになります。
|
||
θは、サーボパルスの基準値からの変位角度であるので、「基準値」と「パルスと角度の割合」に関してはユーザー側で計算しなおす必要があります。
また、足と腰に関しては直交していることが前提となります。(非直交軸に関しては後述) 使い方としては、例えば足の長さ 2a = 200(mm)だった場合。 あと、この計算はmath.hを使って計算するわけですが、マイコンでリアルタイムでやると結構重いです。 |
上記までの計算に基づいた構造のマシンの場合、どんな状態でも常に足の方向が前を向く形になります。 そこにヨー軸を加えることで、足をひねることが出来ます。 その計算について説明します。 |
|
|
ヨー軸を考える 目的のXYZ座標(絶対座標)とヨー軸の角度から、ヨー軸に与える角度と、上記のプログラムに与えるべきXYZ座標(ヨー軸を基準にした相対座標)を極座標平面状で変換します。 γ の位置の足をそのままの状態で γ 時計回りに回転させれば、下図のようになり、前に出した足と比べると、その場で γ だけ回転したように見えます。 簡単に言えば、腰ヨー軸で足裏ヨー軸と同じ働きをさせよう!!ってことです。 |
||||
|
|
|||||
|
|
ヨー軸を計算する まず、移動させたい絶対座標xin、yinを、計算のために極座標に変換する。
γ 足をひねりたいので、欲しい足のひねりを得るθ をγ 分回転させてヨー軸を基準としたXY座標を求める。
このままでは、γ 分多く回転しているので、ヨー軸を反対方向にγ 分回転させて、絶対座標を元に戻す。 ここで、θout はヨー軸に与えられる角度である。
ここで、Z座標には影響しないので
最終的にここではXY座標を求めただけなので、求めた座標をXout、Yout、Zout を「腰を原点とする足のXYZの計算」の計算に放り込 めば、思いのままの足裏XYZ+ヨー軸制御が出来ます。 |
||||
ヨー軸を利用したモジュールの流れはこんな感じ。
また、このヨー軸の計算を用いるには、あくまでも腰の部分で3軸が直交していることが条件になります。 |
最近、膝をダブルサーボにする構成のマシンが増えてきています。 直列につないでいる以上モーメントを分散することは出来ないので、トルクの面よりも、ダブルサーボの良さは「スピード」でしょうか? ジャンプ等のモーションで腰と足首の2サーボが同時動けば、膝は2倍の速度を求められますので、したがって膝に2サーボ必要という具合ですね。 もちろん、腰ピッチと足首ピッチの2倍の速度で高トルクが出力できるのサーボ、が、膝に用意できればダブルサーボにする必要はないですが・・・。 でも、そんなサーボあったらそれを腰と足首に使いますよね(笑)。結果的に膝はダブルサーボが必要という結論に落ち着くんだと思います。
そんなこんなで、ダブルサーボの計算方法をまとめてみました。 |
|
|
結論から言うと膝がシングルサーボの時とダブルサーボの時の計算の違いは α 、β の変数の計算が違うだけです。 膝の計算 腰から足までの直線距離を変数 l とおく。
x,y,zは目標値。 この計算によりダブルサーボの膝は、腰と足首を結んだ直線(l)に常に平行を保ちます。 前述したとおり α 、β 以外の変数は基本的にシングルサーボと同じ考え方でOKです。 |
ここまで、計算を簡略化する便宜上「腰から膝」「膝から足首」の長さは等しいものとする、としてきましたが、実際、設計段階から気をつけていなければ、「腰から膝」「膝から足首」の長さが等しいロボットは少ないでしょう。
そこで、どんな長さのロボットでもこの計算が適用できるように改変したものをここに紹介します。 ヘロンの公式ってなに?って人はこちら |
|
|
違いは α 、βの部分だけです。 ヘロンの公式を用いて膝に出来た三角形の面積を求める
三角形の底辺を l と考えると面積を底辺で割れば高さが求められる
2つの三角形に分けて角度を求めていく
この α 、β 、α' 、β' を用いれば、あとは1章の「膝を原点とする足のXYZの計算」を用いてXYZのモジュールを全てそのまま使用できます。
|
|
腰ピッチの回転が逆転する瞬間の図(黒)
|
また、ここでは直交軸についてしか触れませんでしたが、同じ方法を用いて、直交軸以外のKHR-1や、ROBONOVA-1のようなロボットにも応用することが出来ます。 ポイントは、ピッチ軸は当然足を前後するためにあるのですが、それと同時にピッチ軸には、腰のロール軸と足首のロール軸の距離を制御する役割もあるということです。 この2つの要素を別々に考えることが出来れば、ここで紹介した逆運動学の計算をどんな構造のロボットにでも応用できると思います。 ------------- というわけで、2足歩行ロボットをやる上で、これから逆運動学の計算はどんどん重要になってくると思います。 その重要性をどう伝えようかと考えていたのですが、SISO JUNK STUDIO/ SISO-LABのSISOさんのブログで素晴らしい記事があったのでここに抜粋させていただきます。
なぜ、逆運動学を使わないと安定した歩行ができないかを図で説明されています。 この制御は、角速度一定でプログラムされた教示機能や、ポジションキャプチャリングにはまず不可能なことです。 二足歩行の総合格闘技大会のROBO-ONEに置いても、「相手を倒すアイディア」も重要ですが、それ以上にスリップダウンがダウンにカウントされるようになった今、歩行において既に差は見え始めていると思います。 というわけで、「是非逆運動学を普及させたいな」と思い、この記事を書きました。 とにかく、少しでも興味を持たれましたら、頑張って実装してみてください。
|
|
|
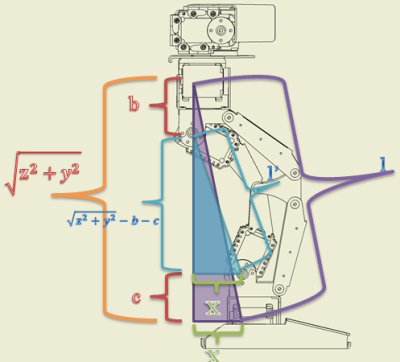
軸と角度の定義 基本的には直交軸によく似ているのですが、腰と足首の関節が直交ではないためb,cの定数を設定します。 また、腰ピッチと足首ピッチを結ぶ直線をl’と定義します。 lは原点とx,y,zの最終的な制御点を結ぶ直線です。 非直交軸の特徴はlとl’が一致しないので、そこを計算に含めるのがポイントです。
|
 |
膝の計算 2つの三角形に注目することがポイントです。
また、この平面はx-z平面ではなく、ピッチ軸に直交する平面上であるという点もポイントです。 これでl’が計算できます。 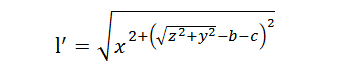 ちなみにlは特に計算する必要はありません。 |
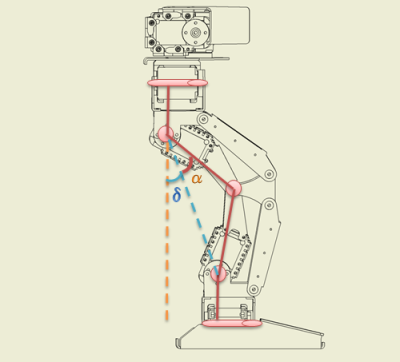 |
ピッチ軸の変位 l’を用いて計算する点を除けば、直交軸と考え方は同じです。 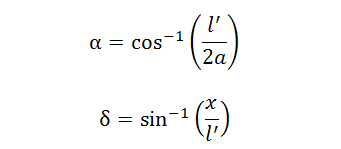 |
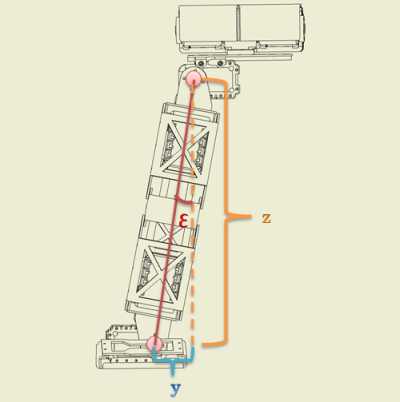 |
ロール軸の角度の決定 また、足裏が地面に平行であるには、ロール方向も同様に ε を計算することが必要 。これは直交軸の時と同じです。 ちなみにこのときはl’ではなくlに注目している点がポイントです。 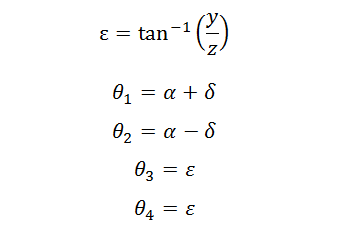 |
ちなみにこの計算を応用すれば、KHR-1やROBONOVA-1、JO-ZERO等多くのキットロボで応用可能です。 ダブルサーボの説明と関節間の長さが違う場合は組み合わせればOKです。 また、アキレスのような膝関節が上下2段になっている平行リンクに関しては、その間隔を定数dと定義した上で、定数b,cと同様に扱うことで制御可能なハズです。 たぶんRB-1000のようなピッチとロールがクロスしているような関節もl'の計算の時にb,cを足すことで簡単に計算できるでしょう。 |
Copyright ©2004-2011 HM(みっちー) All Rights Reserved.